Marketing Mix Modeling (MMM) is a popular measurement technique to understand how different marketing channels and campaigns–as well as non-marketing factors like pricing, product assortment, distribution channel mix, competitive actions, and the macroeconomic environment—affect business outcomes. While there are many technical resources available online describing the statistical models used in MMMs and the pros and cons of each, a straightforward linear Marketing Mix Modeling example—focusing on the data required and the visual and data outputs emerging—is lacking. In this article, we will go through a complete Marketing Mix Modeling example from start to finish.
Use Cases for Marketing Mix Modeling
Marketing mix modeling (MMM) is a specific type of econometric modeling. Econometric modeling is the analysis of data over time and across categories to understand causality and forecast future results. MMMs, at their simplest, explain how marketing activity drives sales. They have many use cases, including estimating the long-run impact of advertising, optimizing marketing spend between channels, understanding audience responsiveness, evaluating campaign effectiveness, forecasting sales, conducting scenario analysis, and measuring overall performance—usually reported as returning on advertising spend or ROAS.
Marketing mix modeling is used across many industries. The most prevalent marketing mix modeling example is in the consumer package goods (CPG) industry. This industry sells mainly through retail distribution, making end customer-level data hard to come by—either for measurement or activation. This means that most marketing is “upper funnel”—video, print, or interactive without a specific call to action. This kind of marketing is ideal for modeling with MMM, as direct attribution is usually impossible.
Soup to Nuts Marketing Mix Modeling Example
Sourcing Data
Marketing mix modeling data can be divided into three basic categories. The vast majority of data are “x” or independent variables. These variables are hypothesized to drive dependent variables. Independent variables can be further sub-divided into control variables and stimulus variables.
Control variables cannot be influenced by the advertising, but still have the potential to explain outcomes. For example, the 10-year Treasury Rate is commonly used as a proxy for credit availability, which can impact consumer demand for more non-essential items. When the rate goes down, credit tends to be cheaper and looser, causing consumers to open their wallets. Conversely, the S&P 500 index is commonly used as a proxy for how wealthy consumers feel; if they have more money in their 401(K)s—even if it will not be available to them for decades—they tend to open their wallets.
Stimulus variables are at least partially controllable by the advertiser. Paid media—think television, digital display and social, paid search, and affiliate marketing—is completely under the control of marketing decisionmakers. Earned media is partially controlled; it takes time for PR and influencer marketing efforts to drive impressions, but companies can still make decisions to increase or decrease focus. Price is also partially controllable; for companies that use third-party distribution channels, setting price is more suggestive, and takes longer to take hold, but it is still a lever. Likewise, overall distribution channel mix is also a longer-term decision, but still has important impacts on marketing performance.
Response variables represent behavior that is affected by marketing. The most common response variable is sales, which can be measured both in dollars and units; either can be used in modeling. More advanced metrics like customer lifetime value (CLV) can also be used in lieu of gross sales.
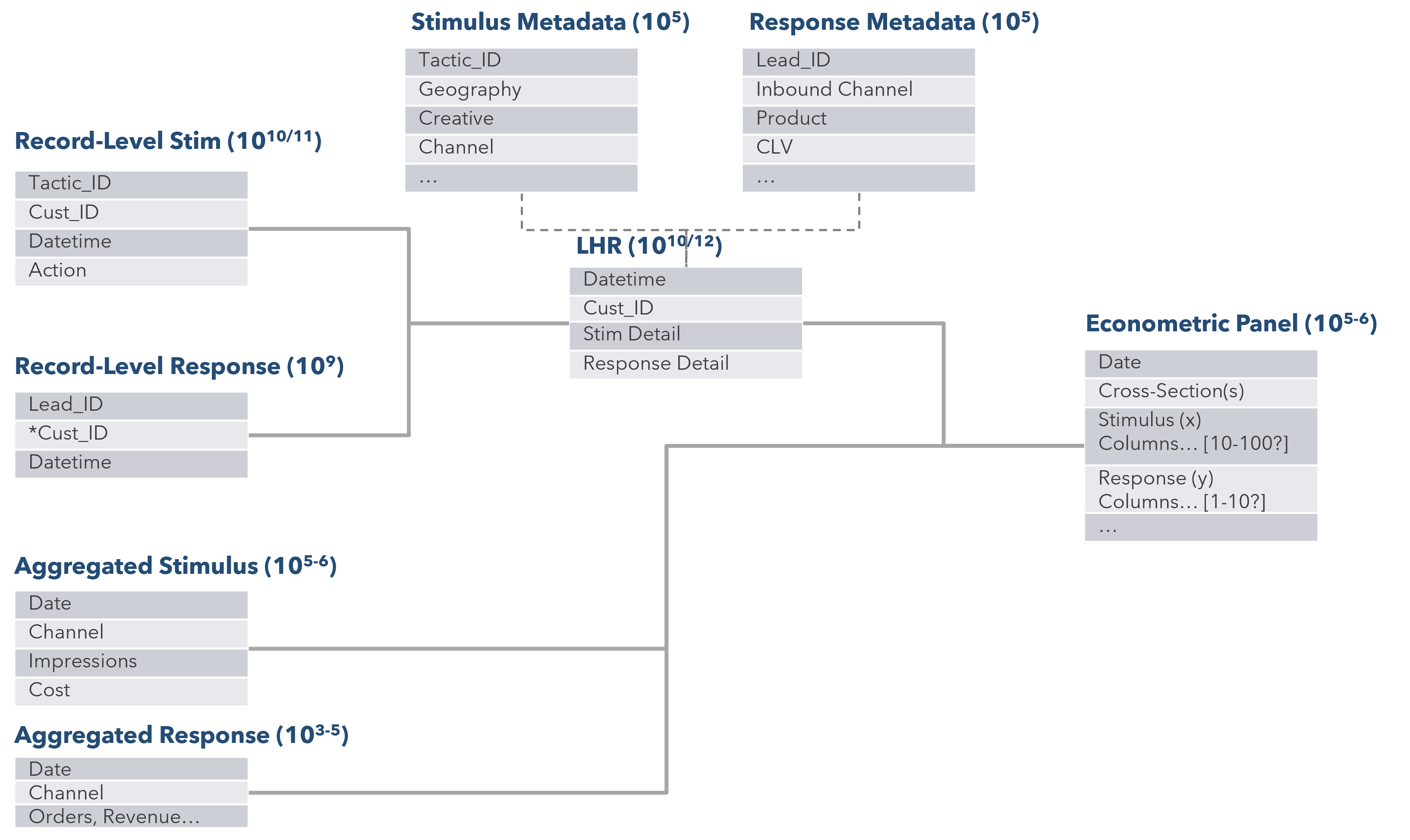
Figure 1: Building the panel using both record-level and aggregated data.
Intermediate response variables that point to constructs like brand equity can also be collected. Both survey-based metrics like brand awareness, comprehension, affinity, or net promoter score and behavioral data like share-of-search, Google trends, and pre-paywall pageviews can be used as intermediate proxies.
Cross-sectional (sometimes called panel) variables organize independent and dependent variables. Cross-sections can include two types of components: a time component (Week or Day) and optional category components (Geographic, audiences, cohorts, etc.) For the econometric time series, each model needs between one to three years’ worth of data. The robustness of a model will increase by uncovering any seasonal trend or impact of outside factors. The goal is to ensure the data spans a period with consistent marketing affecting consumer purchase decisions. Category component data can include geographic areas (e.g., County or DMA), audiences, cohorts (e.g., customer birth dates), or any other relevant grouping criteria. While not necessary, including category components increases the degrees of freedom available and thus the precision and granularity of our estimates.
Once identified, all data sources are merged into a clean “panel” format. The source of each data set is either owned by various parts of an organization (Finance, Sales, Consumer Insights, Digital, IT, Marketing), vendors that support business functions (CRM, Media activation), or open-source information (Credit rate, Consumer Price Index). Communication and alignment between these distinct groups are necessary to set data requirements and ensure consistency. This process—sometimes called extraction, transformation, and loading (ETL)—is typically the most time consuming and error prone step in the process.
Typically, this “data munging” process is first done in batch format. Input files are arranged in a staging area—sometimes something as a simple as a hard disk, but increasingly using a cloud-based storage and compute environment like Databricks. It is best practice to write the data transformation steps in a text-based language like SQL or Python, and store the steps in a version control system like Github. This ETL process can then evolve over time as files change, more APIs are used in place of flat files, and additional data sources are added.
Exploratory Data Analysis and Quality Assurance
One of the most common mistakes beginner MMM modelers make is to jump immediately to regression modeling. However, most “bad” models turn out that way not because of the inferential modeling, but because of quality issues with the underlying data or an incomplete understanding of what the data represents.
Exploratory data analysis (EDA) is also too often a throwaway step that is rushed through to get to the real work. In fact, EDA should be approached with a similar level of rigor that one would use for regression modeling. To achieve this, the analysts involved need to have a clear plan of attack. This plan of attack is best documented with a series of archetype tables with “golden number” results expected.
The goal of any data validation is to make sure the “golden number” tracks through the data transformation step. The challenge here is that executive leadership views the data at a total budget or revenue level. Concurrently, the raw data used to create the panel is at a more granular level (Individual sales or marketing campaign activation). Consistency between how the data is labeled and any difference in timescale (When a marketing campaign is in flight vs. When its paid for) will affect the executive view. The goal in a proper EDA is to make sure that the golden numbers match between the analytics data set and the financial “common knowledge” that executives will use to judge whether the model is to be trusted.
For example, say one desired output table was total end customer revenue by geography by month, for the year 2024. The golden number would be sourced from an agreed-upon executive dashboard or report. Using the econometric time series data set, the analyst would then group by the required dimensions and sum (in this case, something like sum revenue by county by month where year equal 2024.)
Beyond validation, exploratory data analysis can also be helpful when forming hypotheses. Data visualizations like time series plots, bar charts showing counts or sums of independent and dependent variables by year, month or quarter, and scatterplots showing relationships between two variables are some of the most common visualizations used. Having a library of common visualizations in a single workbook (for example, in an Rmarkdown or Jupyter notebook file) is a best practice to rapidly create visualizations from a time series data set. Beyond validation and hypothesis generation, initial learnings from the EDA often help lend credibility to MMM results later during delivery.
Modeling
Before starting the modeling process, it is important to select an appropriate model type, which depends on the nature of the underlying data, and the sophistication of the analysis. In determining model type, there are 3 primary considerations:
- Response shape construction
- Multilevel modeling
- Frequentist vs. Bayesian
Multilevel models can include any of the response shapes discussed and any model can be estimated as either a Frequentist or Bayesian model.
Response Shapes
Response shapes can be as simple or complex as needed for the task. As complexity increases, we trade off ease of training and interpretability for accuracy and flexibility. From simplest to complex, the three common response shapes are linear, non-linear, and splines.
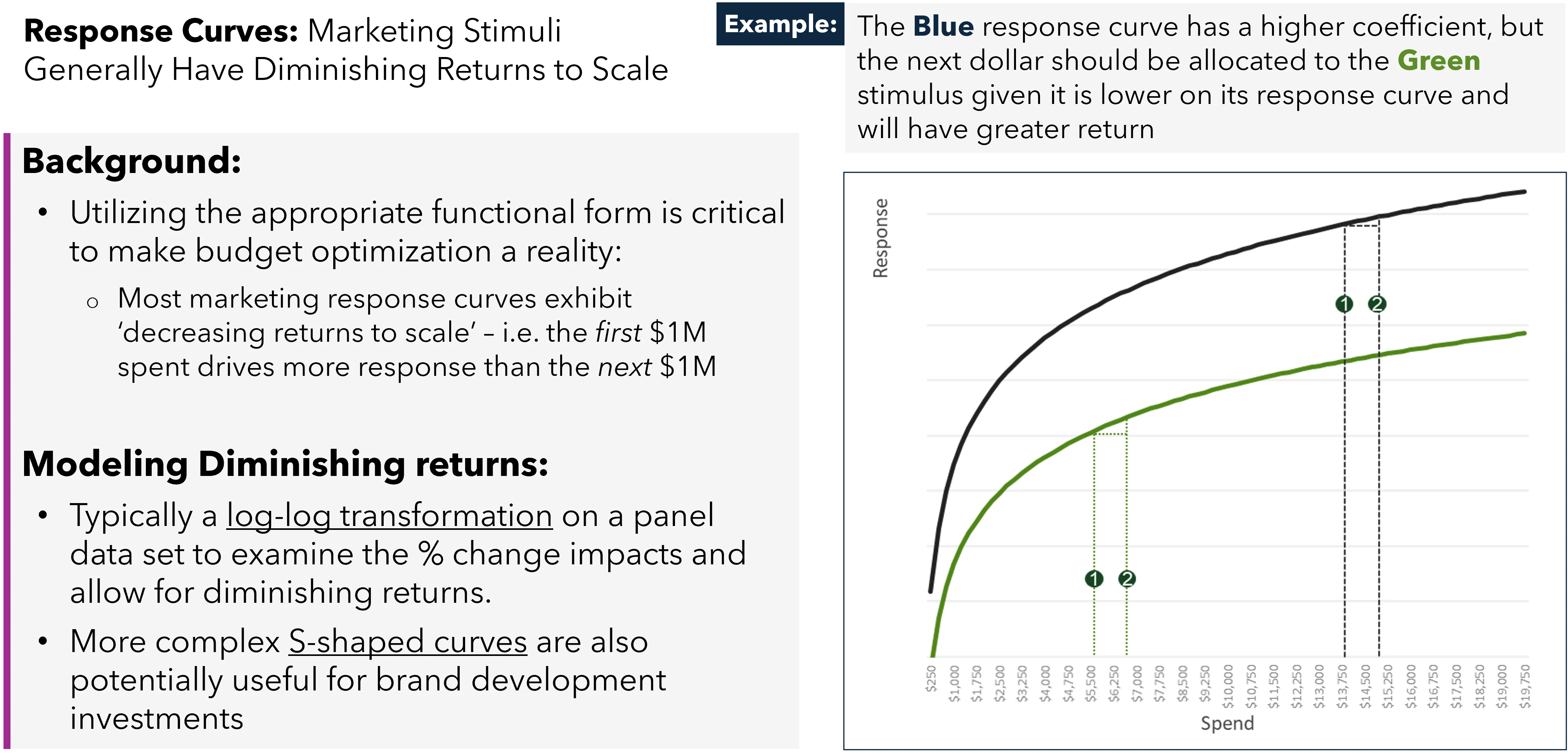
Figure 2: Diminishing returns curves in action.
Linear regression models are linear with respect to the regression parameters (i.e. the betas). This means we can still apply any transformations that do not require additional parameters beyond the classic beta parameters and account for concepts such as diminishing returns. The most common of such are log, square root, and inverse transformations. While useful, these transformations often produce nonsensical results at very low or very high spend due to their lack of flexibility. For example, log transforming both the stimulus and response variables implies constant elasticity—meaning that at any point on the curve (i.e., an amount of marketing spend), the percent change in the response variable divided by the percent change in spend will be the same. In other words, increasing the spend on a marketing channel from $1 to $1.01 results in the same percent increase in sales as going from $1M to $1.01M dollars, which clearly does not represent reality. Nonetheless, linear models are straightforward and easy to interpret, making them suitable for scenarios where we do not expect a complex relationship between stimulus and response variables. They can also be helpful as “back of the envelope” starter models to understand whether a given set of independent variables impact an outcome.
Non-linear models extend linear models by allowing parameters that are not linear with respect to response. This brings the possibility of flexible functional forms that can estimate more realistic diminishing return curves. More advanced approaches are typically used to model the typical “S”-curves seen with upper-funnel advertising. An S-curve shape acknowledges that there is a minimum level of spend below which marketing is ineffective, then the curve rapidly steepens, and then eventually plateaus. While clearly valuable, non-linear models are harder to estimate and thus require more data and training time. This estimation difficulty also typically results in larger parameter confidence intervals.
Generalized additive models further extend modeling capabilities with splines. Splines offer even more flexibility by allowing different polynomial functions (or any other basis function) to be fitted to different segments of the data, ensuring that the model can adapt to varying rates of change in the response variable across different ranges of marketing spend. With this construction, they can theoretically model any smooth response shape including both S-curves and diminishing returns. However, as always there are downsides; without taking care in construction (e.g. applying sufficient regularization) splines often result in nonsensical response shapes (e.g. a response shape that looks like a sine wave) and their nonparametric nature reduces interpretability.
Multilevel Modeling
Mixed models, multilevel models, and panel models all make use of cross-sectional variables and are used interchangeably depending on the domain. Here, we will use the term multilevel models. These cross-sections are often geographies which are used below as a concrete marketing mix modeling example. However, the same statements can be made about any level (e.g. audience or cohort).
Geographical cross-sections provide two dimensions (time and geo) which implies for every point in time, we have many samples (one for each geo) and for every geo, we have many samples (one for each point in time)
This substantially increases the samples in our dataset, increasing the precision of our estimates. Additionally, it opens the door to new modeling techniques. The most common of which are:
- Geo-level response curves: geo-level variation is leveraged to estimate individual response curves by geography either through no pooling (i.e., response curves for a geo are estimated using only data from that geo) or partial pooling (i.e., response curves for a geo are estimated by essentially taking the weighted average of the no pooling estimate and the average estimate across all geos)
- Controlling for unobserved time varying effects: dummies for each point in time can be added to the model as there are multiple samples per point in time (often called time fixed effects)
As always, there is no free lunch:
- The size of the data inherently makes constructing the dataset more difficult and increases training time substantially
- Data is not always available at the geographic level for all channels, requiring assumptions around how that spend should be distributed in creation of the panel
- Geographic labels do not always align between different marketing platforms, making joining arduous and error prone
Frequentist vs. Bayesian
Frequentist regression (i.e., the statistical paradigm most taught and used historically) assumes nothing is known of the relationships of interest prior to collecting and analyzing data. Frequentist regression is solely driven by the data collected.
Bayesian regression, on the other hand, combines prior beliefs (i.e., the prior) with the data (i.e., the likelihood) to compute estimates (i.e., posterior estimates). Priors can conceptually be divided into two types:
- Utility priors: Priors that regularize, helping with multicollinearity and estimation of complex non-linear response curves. As the complexity or granularity of the model increases, utility priors become more necessary.
- Previous knowledge priors: Priors resulting from domain knowledge, benchmarks, or previous modeling exercises
- Experimentation priors: Priors resulting from experimental results, most commonly geo-tests. These are particularly useful for channels with questions around causality (e.g., branded paid search).
Historically, frequentist regression became standard primarily for computational reasons. Parameter estimates and p-values can theoretically be computed by hand or very efficiently with a computer whereas Bayesian estimates are usually impossible to compute via hand and time-intensive on a computer. Increasing computational power has closed the gap; however, Bayesian regression models still take much longer to train and iterate.
Variable Selection
Almost any combination of independent variables could be added to a model, but getting to the right structure is an iterative process that demands careful consideration. The structure of a marketing mix model requires a thoughtful approach to selecting and including the right combination of independent variables. This iterative process demands careful consideration because the wrong combination of variables, omitted variables, or an imbalance in the number of variables can lead to problematic model structures. Including too many variables can make the model overly complex and difficult to interpret, while too few variables might result in an oversimplified model that lacks actionability.
Feature selection requires a mix of necessary business variables and leveraging scientific methods to decide variable importance. Any factor that has an indirect impact on sales could be of value from the business perspective. Examples might include the effect of a new campaign for a specific product or measuring the impact of a change in sales channel.
How potential customers interact with marketing stimuli before they make a purchase decision should also be considered. Customers engage with several types of marketing stimuli while in the marketing funnel. The marketing funnel consists of four stages (awareness, interest, engagement, and conversion). For example, TV would be considered a channel driving awareness while paid search would be a conversion channel. How variables interact must be considered before a correlation matrix is used for potential variable selection. A correlation matrix is typically the first step in identifying candidate significant variables. This matrix displays the correlations between all pairs of variables and can be enhanced with color shading to indicate high positive or high negative correlations, making it easier to spot potentially powerful independent variables. High correlations between variables suggest multicollinearity, a situation where two or more variables are highly correlated and provide redundant information. Multicollinearity can inflate the variance of coefficient estimates and make the model unstable. Therefore, identifying and addressing multicollinearity is crucial in the early stages of model building.
Variable reduction is often necessary, especially when using non-Bayesian modeling approaches with many different stimulus variables that are co-linear. Co-linearity occurs when changes in one advertising lever are accompanied by changes in others. This can lead to counterintuitive results, such as variables that should have positive coefficients turning negative. To mitigate this issue, analysts employ techniques like correlation analysis, variance inflation factors (VIF), and principal component analysis (PCA) to reduce the number of variables while retaining the essential information.
Stepwise regression is a systematic technique for variable selection that can help in building a parsimonious model. This method involves adding and removing variables iteratively based on their statistical significance in explaining the response variable. Forward selection starts with no variables in the model, adding one variable at a time, while backward elimination starts with all candidate variables and removes the least significant ones step by step. Stepwise regression balances between these two approaches, adding and removing variables as needed to optimize the model’s performance.
Regularization techniques like Lasso (Least Absolute Shrinkage and Selection Operator) and Ridge Regression are essential for reducing overfitting. Overfitting occurs when a model is too complex and captures the noise in the data rather than the underlying relationship. Lasso adds a penalty equal to the absolute value of the magnitude of coefficients, effectively reducing some coefficients to zero and thus performing variable selection. Ridge Regression adds a penalty equal to the square of the magnitude of coefficients, shrinking all coefficients towards zero but never setting them exactly to zero. Elastic Net combines both Lasso and Ridge penalties, providing a balance that can be particularly useful in situations with highly correlated predictors. Each of these methodologies helps refine the model structure, ensuring it is both robust and interpretable. By iterating through these steps, analysts can develop a model that accurately captures the relationships between marketing activities and business outcomes, providing actionable insights for optimizing marketing strategies.
Evaluating the Model
Evaluating a Marketing Mix Model’s (MMM) performance involves two main components: model fit and prediction. Four key traits should always be considered:
- Accurately represents reality
- Accuracy of prediction for out-of-sample periods
- Measured relationship of marketing variables + external factors
- Provides meaningful decision-making insights
These traits ensure that the model is both statistically sound and practically useful.
The first validation step for any model is to review any diagnostic checks such as residual analysis. Residual analysis involves examining the residuals (the differences between observed and predicted values) to check for homoscedasticity (constant variance), autocorrelation (residuals are not correlated over time), and normality (residuals follow a normal distribution). Evaluating residuals over time helps identify unobserved effects which may significantly bias results. These checks help ensure that the model assumptions hold true and that the model provides a reliable representation of reality.
To validate if a model has accurately inferred an underlying pattern from actual data (Model fit), we can use the R-squared metric. The R-squared value measures the proportion of variance in the dependent variable predictable from the independent variables. R-squared can be misleading in complex models so it makes more sense to use an Adjusted R-squared since it adjusts for the number of predictors in the model.
When trying to compare different models, one can use the Akaike Information Criterion (AIC) or Bayesian Information Criterion (BIC) with a lower value indicating a better model. These criteria penalize models with more parameters, thus discouraging overfitting.
For example, a model that produces better fit metrics such as R-squared and BIC but fails to meet model assumptions is worse for inference than one with a lesser fit that meets model assumptions.
The gold standard for measuring a model’s ability to accurately predict unseen data is the out-of-sample mean absolute percentage error (MAPE). This metric assesses the prediction accuracy by comparing the predicted values to the actual values in out-of-sample data. Out-of-sample testing involves splitting the data into a training set and a hold-out set. The model is trained on the training set and then tested on the hold-out set to evaluate its generalizability. Cross-validation techniques, such as k-fold cross-validation, extend out-of-sample testing. In k-fold cross-validation, the data is divided into k subsets, and the model is trained on k-1 subsets while the remaining subset is used for testing. This process is repeated k times, with each subset used exactly once for testing. With time series data, these folds are often split such that training folds precede testing folds temporally. These methods help ensure that the model is not overfitted to the training data and can generalize well to new data. Care still needs to be taken in optimizing purely against out-of-sample performance. A model that predicts well is not useful for inference if it does not properly uncover the relationships between stimulus and response.
Perhaps the most important validation is common sense, known as “face validity.” This involves ensuring that the model makes sense from a business perspective and aligns with known market behaviors and historical insights. For example, if the model suggests that a particular marketing channel has a huge impact on sales, but this contradicts known business practices or historical performance, then the model may need to be re-evaluated. Business validation involves discussing the model results with stakeholders who have domain expertise to confirm that the results are reasonable and actionable. This step is crucial because a model that is statistically sound but lacks practical relevance is of little use. Face validity checks ensure that the model’s insights are grounded in reality and can be used to inform strategic decision-making.
Presenting and Using the Results
Once a model has been built and validated, the last step is using it to inform, predict, and make decisions. This involves communicating the insights effectively, integrating the model into business intelligence tools, and potentially leveraging the model for optimization.
PowerPoint
Even though data scientists hate to admit it, PowerPoint is still the lingua franca of business. Almost every MMM project ends with at least one PowerPoint. Ideally, two decks will be created: a “walking” deck meant to be read, and a “presentation” deck meant to be discussed. Too often, this isn’t the case, and the dense walking deck is read out to executives; this is probably the number one pitfall when communicating MMM results.
Either deck will still have the same basic sections:
- Background and Objectives: Data scientists and statisticians often overlook explaining what the goal of the entire MMM process is, and generally how econometric modeling works. While this section can be skipped over in later “runs” of the model, it is important to set the stage for executives, outlining how regression works, what it is good for (understanding holistic relationships between marketing channels and long-run strategy) and not good for (immediate decision-making and quick campaign reads), and how it will be used as it evolves.
- Model Overview: This section explains the model type, the variables included, and the rationale behind their selection. While these slides can be very technical, it is typically best to move most of the technical background to an appendix that can be referenced if needed, and to instead focus on the 30,000-foot view in the main executive summary. Structural equation-type diagrams can be used to illustrate the model structure at a high level and the relationships between variables.
- Data Insights: Exploratory data analysis, while not the main topic of an MMM, is typically used to validate and tie to “golden numbers,” ensuring executive buy-in that the data used to build the model itself are correct. In addition to validating golden numbers, interesting trends and insights that fall outside of the scope of the model itself can be explored in this section.
- Model Outputs: This section is the “meat of the sandwich,” in which model outputs are concisely communicated. This section should communicate total marketing contribution; overall ROAS (return on advertising spend) and cost-per-acquisition (CPA); channel-by-channel contributions, again outputting both ROAS and CPA; marginal CPA and ROAS; channel-specific adstocks (how long a channel’s influence is felt in-market); and response curves by channel.
- Predictions and Scenarios: This section helps stakeholders understand the “so what” of the analysis—the normative “what we should do.” Typically, forecasts and scenario analyses based on the model are created. There are literally infinite scenarios possible, so choosing which to highlight requires coordination between the team doing the work and the marketers making the big future decisions. Regardless of the specific scenarios picked, the presentation should highlight how different levels of marketing spend or other variables impact outcomes.
Business Intelligence (BI) Tools
Integrating MMM results into business intelligence (BI) tools allows for continuous monitoring and analysis. BI tools such as Tableau, Power BI, or QlikView can be used to create interactive dashboards that update in real time as new data becomes available. This integration is definitely a later step for most companies, as it requires data engineering and technical steps beyond just displaying outputs in PowerPoint.
To make marketing mix models play nicely with BI outputs, there need to be consistent output data structures. Typically, an output data structure that includes standard time and cross-sectional dimensions—the same as those used in the time series panel, along with key “facts”—contributions, cost-pers, and ROAS.
Decision Support
Because of their underlying architecture, MMMs are natural candidates for use in decision support and optimization. Marketing mix models include non-linear, diminishing returns curves by their nature; optimization is a matter of finding the ideal mix of curves that maximizes a certain objective function—for example, maximizing revenue—subject to a set of constraints.
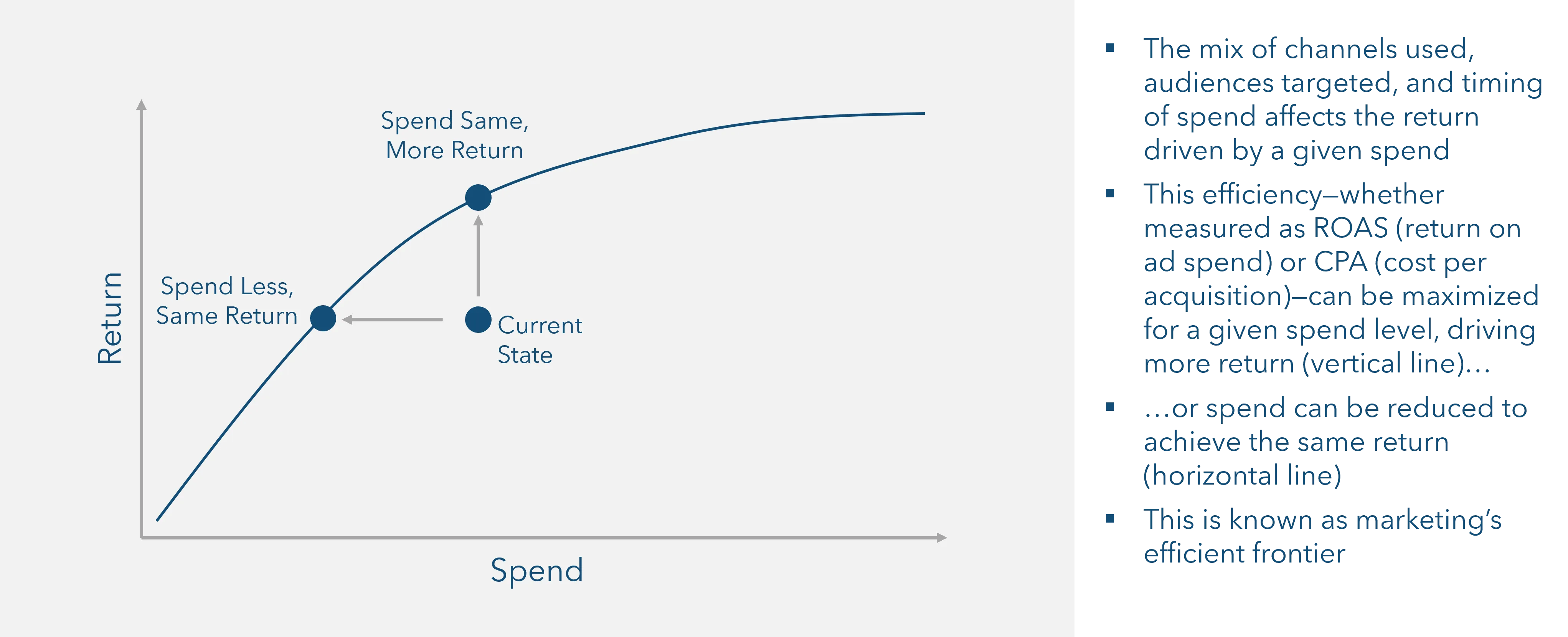
Figure 3: Optimization is about re-mixing marketing channels to achieve the best efficiency at a given level of spend
The simplest way to support this optimization exercise is to use a built-in linear programming algorithm such as Microsoft Excel’s Solver. In this approach, each curve can be extracted as an equation, and then aggregate outputs can be assigned to certain cells. One cell can be made the objective, and others can be assigned as constraints—for example, TV spend must be less than 30% of mix, the total investment must be less than $100M, and so forth. More advanced approaches can use machine learning algorithms in R and Python to optimize mixes.
Conclusion: Marketing Mix Modeling Example
Marketing mix modeling is sometimes seen as an intimidating and mythical black box by marketers and non-technical business professionals, which can lead to low trust in results. This need not be the case. Even non-technical managers should understand the steps taken to build and output an MMM. By presenting a clear Marketing Mix Modeling example, I illustrated how various marketing channels and external factors intertwine to affect business outcomes. This marketing mix modeling example serves as a valuable reference for understanding how data-driven decisions can enhance marketing effectiveness and drive success.

Download our whitepaper, “Measuring Marketing’s Effectiveness”
Access our whitepaper for a deep dive into additional imperatives and methods for CMOs and analytics teams driving measurable marketing ROI.



